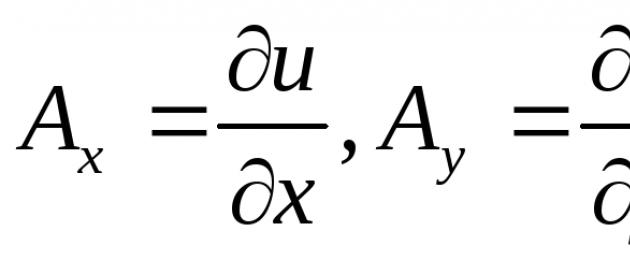Определение 27. Векторное поле A = {A x , A y , A z } называется потенциальным , если вектор А является градиентом некоторой скалярной функции u = u (x , y , z ) :

A = grad u = . (119)

При этом функция и называется потенциалом данного векторного поля.

Примерами потенциальных полей являются поле тяготения точечной массы т , помещенной в начале координат, электрическое поле точечного заряда е , находящегося в начале координат, и другие.

Выясним, при каких условиях векторное поле является потенциальным.

Так как из (119) следует, что
то

так как смешанная производная второго порядка не зависит от порядка дифференцирования. Из этих равенств легко получаем, что

rot A = 0 – (120)

условие потенциальности векторного поля.

Определение 28. Векторное поле A = {A x , A y , A z }, для которого rot A = 0, называется безвихревым .

Из предыдущих рассуждений следует, что любое потенциальное поле является безвихревым. Можно доказать и обратное, то есть то, что любое безвихревое поле есть поле потенциальное.

Пример 30 .

Определить, является ли векторное поле потенциальным. В случае положительного ответа найти его потенциали в предположении, что в начале координат и = 0.

Вычислим частные производные функций ,

Следовательно,
то естьrot F = 0 – выполнено условие (120), и поле является потенциальным.

8. Соленоидальные и гармонические векторные поля

Определение 29. Векторное поле A = {A x , A y , A z } называется соленоидальным в области D , если в каждой точке этой области

div A = 0. (121)

Замечание . Так как дивергенция характеризует плотность источников поля А , то в области, где поле соленоидально, нет источников этого поля. Примером соленоидального поля может служить поле точечного заряда е во всех точках, кроме точки, где расположен заряд.

Условием соленоидальности поля является требование, что вектор А является ротором некоторого вектора В : A = rot B . Докажем это.

Действительно, если , то

div A =

Определение 30. Скалярное поле, задаваемое функцией u = u (x , y , z ) , называется гармоническим в некоторой области, если функция и в этой области удовлетворяет уравнению Лапласа: Δ и = 0.

Примеры: линейная функция, потенциал электрического поля точечного заряда или поля тяготения точечной массы.

Литература

Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Наука, 1969.

Кудрявцев Л.Д. Краткий курс математического анализа. М.: Наука, 1989.

Ильин В.А., Позняк Э.Г. Математический анализ. М.: Наука, 1999.

Смирнов В.И. Курс высшей математики.- Т.2. М.: Наука, 1965.

Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 1981.

Пискунов Н.С. Дифференциальное и интегральное исчисление. – Т.2. М.: Наука, 1981.

Сборник задач по математике для втузов. Специальные разделы математического анализа (под редекцией А.В.Ефимова и Б.П.Демидовича). – Т.2. М.: Наука, 1981.

Мышкис А.Д. Лекции по высшей математике. М.: Наука, 1973.

Теорема 1. Для того, чтобы векторное поле, заданное в области Т, было соленоидальным, необходимо и достаточно, чтобы это поле было полем ротора некоторого вектора, т.е. чтобы существовал вектор, во всех точках области Т удовлетворяющий условию

Доказательство.

Достаточность. Имеем

Необходимость. Пусть

Найдем функцию, такую, что

Ниже мы покажем, что функция определяется неоднозначно, поэтому на эту функцию можно наложить дополнительные условия. Пусть

Выберем функции

Покажем, что эти функции удовлетворяют системе уравнений (1). Действительно имеем

Действительно, построенная функция удовлетворяет условию

Функцию называют векторным потенциалом.

При доказательстве теоремы мы предложили метод, позволяющий определять векторный потенциал поля.

Замечание 1. Если функция является векторным потенциалом поля, то функция

где - произвольная скалярная функция, также является векторным потенциалом поля.

Доказательство.

Следовательно, векторный потенциал определяется неоднозначно.

Пример 1. Показать, что поле

Решение. Имеем.

Вычислим

Найденная функция является искомым векторным потенциалом. Проверим это утверждение, т.е. найдем ротор:

Условие выполнено. Нетрудно проверить, что векторным потенциалом этого поля может быть более симметричная функция

Пример 2. Показать, что поле

соленоидально и найти векторный потенциал этого поля.

Решение. Имеем.

Вычислим

Проверим:

Условие выполнено. Нетрудно проверить, что векторным потенциалом этого поля могут быть более симметричные функции

Из приведенных примеров видно, что выражения для векторного потенциала для одного и того же поля могут заметно различаться. Это связано с тем, что к найденному векторному потенциалу можно добавить градиент любой скалярной функции.

Определение 1. Пусть А - векторное поле в области Функция называется потенциалом поля А в области если в этой области

Определение 2. Поле, обладающее потенциалом, называется потенциальным полем.

Поскольку в связной области частные производные определяют функцию с точностью до константы, то в такой области потенциал поля определен с точностью до аддитивной постоянной.

В первой части курса мы уже вскользь говорили о потенциале. Здесь мы обсудим это важное понятие несколько подробнее. Отметим в связи с данными определениями, что в физике при рассмотрении разного рода силовых полей потенциалом поля обычно называют такую функцию что Такой потенциал отличается от введенного определением 1 только знаком.

Пример 1. Напряженность гравитационного поля, создаваемого помещенной в начало координат точечной массой М, в точке пространства, имеющей радиус-вектор вычисляется по закону Ньютона в виде

Это сила, с которой поле действует на единичную массу в соответствующей точке пространства. Гравитационное поле (1)

потенциально. Его потенциалом в смысле определения 1 является функция

Пример 2. Напряженность Е электрического поля точечного заряда помещенного в начале координат, в точке пространства, имеющей радиус-вектор вычисляется по закону Кулона

Теоретический материал по данной теме изложен на с. 228-236 данного издания.

Пример 30 . Проверить, является ли векторное поле

а) потенциальным; б) соленоидальным. Если поле потенциально, найти его потенциал.

Решение. А) Находим ротор поля

Следовательно, поле - потенциально.

Б) Найдем дивергенцию поля

Следовательно, поле не соленоидально.

В) Так как , то потенциал поля может быть вычислен по формуле

Криволинейный интеграл от полного дифференциала не зависит от пути интегрирования. Здесь за начальную точку удобно взять начало координат . В качестве пути интегрирования возьмем ломаную ОАВМ (рис. 17).

Рис. 17

1. На отрезке следовательно

2. На отрезке отсюда

3. На отрезке отсюда

Итак, где - произвольная постоянная.

Окончательно,

Задания на контрольные работы № 5-8

Номера задач выбираются по таблице в соответствии с последними двумя цифрами шифра и первой буквой фамилии. Например, студент Иванов, шифр 1-45-5815, решает в контрольной работе 5 задачи 5, 15, 21,31, в контрольной работе 6 - задачи 45, 51, 61, 71, в контрольной работе 7 - задачи 85, 91, 101, 111, в контрольной работе 8 - задачи 125,135,141,151.

Последняя цифра шифра
Номер контрольной работы
Предпоследняя цифра шифра
Номер контрольной работы
Первая буква фамилии	А,И Т	Б,ОЦ	В,НХ	Г,ФЯ	Д,ЗЛ	Е,МР	Ж,СЧ	К Э	П Щ	У,ШЮ
Номер контрольной работы

Контрольная работа №5

В задачах 1-10 найти общее решение дифференциального уравнения первого порядка

В задачах 11-20 найти общее решение или общий интеграл дифференциального уравнения второго порядка

В задачах 21-30 найти общее решение линейных уравнений второго порядка

В задачах 31-40 найти область сходимости степенных рядов

Контрольная работа №6

В задачах 41-50 разложить функцию в ряд Маклорена, определить область сходимости ряда

В задачах 51-60 построить область интегрирования и изменить порядок интегрирования

61. Вычислить площадь поверхности части сферы , вырезанной цилиндром и плоскостью .

62. Вычислить площадь плоской пластины, ограниченной линиями: и (вне параболы).

63. Вычислить площадь поверхности цилиндра, , отсеченной плоскостями .

64. Найти объем тела, ограниченного поверхностями , , , , .

65. Найти объем тела, ограниченного поверхностями: и , лежащего в I октанте при .

66. Найти площадь плоской пластины, ограниченной линиями , .

67. Определить площадь части круга , находящейся вне круга (использовать полярные координаты).

68. Вычислить массу однородной плоской пластины (),

ограниченной окружностью и прямыми и .

69. Найти массу пластины с плотностью , ограниченную линиями , , .

70. Найти массу пластины с плотностью , заданной неравенствами: .

В задачах 71-80 вычислить криволинейные интегралы по кривой :

Контрольная работа №7

В задачах 81-86 разложить функции в ряд Фурье; построить график заданной функции

81.

82.

83.

84.

85.

86.

В задачах 87, 88 разложите функцию в ряд Фурье по синусам; постройте график заданной функции.

87.

88.

В задачах 89,90 разложите функцию в ряд Фурье по косинусам; постройте график заданной функции.

89.

90.

В задачах 91-95 решить методом Фурье волновое уравнение на заданном отрезке с граничными условиями и заданными начальными условиями.

91.

93.

95.

В задачах 96-100 решить методом Фурье уравнение теплопроводности на данном отрезке при заданном начальном условии и граничных условиях .

96.

97.

98.

99.

100.

В задачах 101-106 вычислить тройной интеграл по области T , заданной неравенствами. Сделать чертеж.

103.
(при вычислении интегралов перейдите к цилиндрическим координатам).

105. (при вычислении интегралов перейдите к цилиндрическим координатам).

В задачах 107-110 найти массу тела, заданного неравенствами и имеющего заданную плотность . Сделать чертеж.

108. (при вычислении тройного интеграла перейти к цилиндрическим координатам).

110. (при вычислении тройного интеграла перейти к цилиндрическим координатам).

В задачах 111-120 вычислите поверхностный интеграл. Сделайте чертеж поверхности.

111. где - часть плоскости ограниченная координатными плоскостями.

112. - верхняя сторона части параболического цилиндра , ограниченная круговым цилиндром и плоскостью . При вычислении интеграла по перейдите к полярным координатам.

113. - часть поверхности цилиндра , ограниченная плоскостями

114. , где - часть поверхности конуса , ограниченная плоскостями и (при вычислении двойного интеграла перейдите к полярным координатам).

115. , - часть кругового цилиндра , ограниченная плоскостями

116. - верхняя сторона части конуса , ограниченной плоскостями . При вычислении интеграла по перейти к полярным координатам.

117. , где - верхняя сторона части сферы . При вычислении двойного интеграла перейдите к полярным координатам.

118. , где - верхняя сторона части плоскости , ограниченной координатными плоскостями.

119. , - часть параболического цилиндра ограниченная координатными плоскостями и плоскостью .

120. ; - верхняя сторона части кругового цилиндра , ограниченная круговым цилиндром и плоскостью Перейдите к полярным координатам.

Контрольная работа № 8

В задачах 121-130 найдите градиент скалярного поля и проверьте, является ли скалярное поле гармоническим.

В задачах 131-135 найдите поток векторного поля через часть поверхности , лежащую в первом октанте в направлении нормали, образующей острый угол с осью . Сделайте чертеж.

В задачах 136-140 вычислите с помощью теоремы Остроградского поток векторного поля в сторону внешней нормали через поверхность тела, лежащего в первом октанте и ограниченного заданной поверхностью и координатными плоскостями. Сделайте чертеж.

В задачах 141-150 вычислите циркуляцию векторного поля по пути пересечения с координатными плоскостями той части поверхности , которая лежит в первом октанте . - точки пересечения поверхности с осями соответственно. Сделайте чертеж.

В задачах 141-145 вычислите циркуляции с помощью теоремы Стокса.

В задачах 146-150 вычислите циркуляцию с помощью ее определения.

В задачах 151-160 проверьте является ли векторное поле : а) потенциальным, б) соленоидальным. Если поле потенциально, найдите его потенциал.

152.

155.

Текущий контроль

Тестовые задания

1. Определить какое уравнение имеет следующее решение .

а) б) в)

2. Определите характеристическое уравнение для дифференциального уравнения

а) б) в)

3. Определить при каком значении будет сходиться степенной ряд по признаку Даламбера .

4. Сформулируйте геометрическую интерпретацию двойного интеграла.

5. Сформулируйте геометрическую интерпретацию тройного интеграла.

6. Определите признак потенциальности векторного поля :

а) б) в)

Итоговый контроль

Вопросы для подготовки к экзамену по математике

(III семестр)

Дифференциальные уравнения

1. Определение обыкновенного дифференциального уравнения, его порядка и решения. Дифференциальное уравнение первого порядка, поле направлений, изоклины.

2. Задача Коши для дифференциального уравнения первого порядка. Теорема существования и единственности решения задачи Коши.

3. Определение общего и частного решения (интеграла) дифференциального уравнения первого порядка.

4. Уравнение с разделяющимися переменными, его интегрирование.

5. Линейное уравнение первого порядка, его интегрирование.

6. Однородное дифференциальное уравнение первого порядка, его интегрирование.

7. Дифференциальное уравнение n -го порядка. Задача Коши для дифференциального уравнения n -го порядка. Теорема существования и единственности решения задачи Коши для уравнения n -го порядка.

8. Определение общего и частного решения дифференциального уравнения n -го порядка. Интегрирование уравнения вида .

9. Уравнения, допускающие понижение порядка. Метод интегрирования уравнения вида , где k < n.

10. Метод интегрирования уравнения вида .

11. Определение линейного дифференциального уравнения n -го порядка. Однородное линейное уравнение. Свойства решений однородного линейного уравнения.

12. Определение линейно-зависимых и линейно-независимых функций. Примеры.

13. Определение фундаментальной системы решений линейного однородного уравнения. Теорема о структуре общего решения линейного однородного уравнения n -го порядка.

14. Теорема о структуре общего решения линейного неоднородного уравнения n -го порядка.

15. Линейное однородное уравнение с постоянными коэффициентами. Метод Эйлера, характеристическое уравнение.

16. Построение фундаментальной системы решений и общего решения линейного однородного уравнения n -го порядка в случае вещественных различных корней характеристического уравнения. Пример.

17. Построение фундаментальной системы решений и общего решения линейного однородного уравнения n -го порядка в случае комплексно-сопряженных корней характеристического уравнения. Пример.

18. Построение фундаментальной системы решений и общего решения линейного однородного уравнения n -го порядка в случае вещественных равных корней характеристического уравнения. Пример.

19. Правило нахождения частного решения линейного неоднородного уравнения с постоянными коэффициентами, если правая часть имеет вид , где - многочлен степени .

20. Правило нахождения частного решения линейного неоднородного уравнения с постоянными коэффициентами, если правая часть имеет вид , где .

21. Метод решения линейного неоднородного дифференциального уравнения вида (принцип наложения).

22. Система линейных дифференциальных уравнений в нормальной форме. Задача Коши. Теорема существования и единственности решения задачи Коши. Определение общего и частного решения системы. Метод исключения для нормальных систем дифференциальных уравнений.

23. Системы линейных дифференциальных уравнений. Свойства решений. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.

Ряды

24. Числовые ряды. Определение n -ой частичной суммы ряда. Понятия сходимости и расходимости числового ряда. Сумма сходящегося ряда. Геометрический ряд.

25. Свойства сходящихся рядов: умножение ряда на число, почленное сложение рядов.

26. Остаток ряда. Теорема об одновременной сходимости ряда и его остатка.

27. Необходимый признак сходимости ряда. Иллюстрация его недостаточности на примере.

28. Положительные ряды. Необходимое и достаточное условие сходимости положительного ряда.

29. Первый и второй признаки сравнения положительных рядов.

30. Признак Даламбера.

31. Интегральный признак Коши.

32. Обобщенный гармонический ряд , где p – любое действительное число. Поведение ряда при p <1, p =1, p >1.

33. Знакопеременные ряды. Абсолютная и неабсолютная сходимость. Теорема о сходимости абсолютно сходящегося ряда.

34. Признак Лейбница сходимости знакочередующегося ряда. Оценка абсолютной погрешности при замене суммы сходящегося ряда суммой первых n

42. Биномиальный ряд для функции .

Замена переменных в тройном интеграле. Примеры: случаи цилиндрических и сферических координат.

Вычисление площади гладкой поверхности, заданной параметрически и в явном виде. Элемент площади поверхности.

Определение криволинейного интеграла первого рода, его основные свойства и вычисление.

Определение криволинейного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.

Формула Грина. Условия того, что криволинейный интеграл на плоскости не зависит от пути интегрирования.

Определение поверхностного интеграла первого рода, его основные свойства и вычисление.

Определение поверхностного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.

Теорема Гаусса-Остроградского, её запись в координатной и векторной (инвариантной) формах.

Теорема Стокса, её запись в координатной и векторной (инвариантной) формах.

Условия того, что криволинейный интеграл в пространстве не зависит от пути интегрирования.

Скалярное поле. Градиент скалярного поля и его свойства. Вычисление градиента в декартовых координатах.

Определение векторного поля. Поле градиента. Потенциальные поля, условия потенциальности.

Поток векторного поля через поверхность. Определение дивергенции векторного поля и её свойства. Вычисление дивергенции в декартовых координатах.

Соленоидальные векторные поля, условия соленоидальности.

Циркуляция векторного поля и ротор векторного поля. Вычисление ротора в декартовых координатах.

Оператор Гамильтона (набла), дифференциальные операции второго порядка, связь между ними.

Основные понятия, относящиеся к оду первого порядка: общее и частное решения, общий интеграл, интегральные кривые. Задача Коши, её геометрический смысл.

Интегрирование оду первого порядка с разделяющимися переменными и однородных.

Интегрирование линейных оду первого порядка и уравнений Бернулли.

Интегрирование оду первого порядка в полных дифференциалах. Интегрирующий множитель.

Метод введения параметра. Интегрирование оду первого порядка Лагранжа и Клеро.

Простейшие оду высших порядков, интегрируемые в квадратурах и допускающие понижение порядка.

Нормальная форма системы линейных оду, скалярная и векторная (матричная) запись. Задача Коши для нормальной системы линейных оду, её геометрический смысл.

Линейно-зависимые и линейно-независимые системы вектор-функций. Необходимое условие линейной зависимости. Теорема об определителе Вронского решений системы однородных линейных оду.

Теорема об общем решении (о структуре общего решения) нормальной системы неоднородных линейных оду.

Метод вариации произвольных постоянных для отыскания частных решений нормальной системы неоднородных линейных оду.

Фундаментальная система решений нормальной системы однородных линейных оду с постоянными коэффициентами в случае простых действительных корней характеристического уравнения.

Линейно-зависимые и линейно-независимые системы функций. Необходимое условие линейной зависимости. Теорема об определителе Вронского решений однородного линейного оду.

Теорема об общем решении (о структуре общего решения) однородного линейного оду.

Теорема об общем решении (о структуре общего решения) неоднородного линейного оду.

Метод вариации произвольных постоянных для отыскания частных решений неоднородного линейного оду.

Фундаментальная система решений однородного линейного оду с постоянными коэффициентами в случае простых корней характеристического уравнения, действительных или комплексных.

Фундаментальная система решений однородного линейного оду с постоянными коэффициентами в случае, когда имеются кратные корни характеристического уравнения.

Отыскание частных решений неоднородного линейного оду с постоянными коэффициентами и специальной правой частью.

Теорема существования (локальная) решения задачи Коши для оду первого порядка.

Теорема единственности решения задачи Коши для оду первого порядка.

1. Определение векторного поля. Поле градиента. Потенциальные поля, условия потенциальности.

Векторное поле. Если каждой точке М некоторой области V пространства соответствует значение некоторой векторной величины (M ), то говорят, что в области V задано векторное поле (M ). Примеры векторных полей – поле тяготения, поля электрической и магнитной напряжённостей, поле скоростей частиц движущейся жидкости.

Если в некоторой декартовой системе координат вектор (M ) имеет координаты Р (M ), Q (M ), R (M ), то . Таким образом, задание векторного поля (M ) эквивалентно заданию трёх скалярных полей Р (M ), Q (M ), R (M ). Будем называть векторное поле гладким , если его координатные функции - гладкие скалярные поля.

Градиентом дифференцируемого скалярного поля u(M)=u(x,y,z) называется вектор . Т.е. сумма частных производных умноженных на соответствующие единичные вектора.

В общем случае градиент вводится как векторная характеристика скалярного поля - то есть области, каждой точке которой соответствует значение определенного скаляра. Градиент характеризует, насколько быстро меняется скалярная величина в том или ином месте этого поля.

Потенциальные векторные поля. Векторное поле A = {Ax, Ay, Az} называется потенциальным, если вектор А является градиентом некоторой скалярной функции u = u(x, y, z): A = grad u = (16.7).

При этом функция u называется потенциалом данного векторного поля.

Выясним, при каких условиях векторное поле является потенциальным . Так как из (16.7) следует, что , То,=,=. так как смешанная производная второго порядка не зависит от порядка дифференцирования. Из этих равенств легко получаем, что rot A = 0 -условие потенциальности векторного поля .

Ротором векторного поля (M ) в точке называется векторная величина (векторное поле):. Если выразитьчерез оператор Гамильтона набла:равен векторному произведению. Действительно,.

1. Поток векторного поля через поверхность. Определение дивергенции векторного поля и её свойства. Вычисление дивергенции в декартовых координатах.

Поток векторного поля через поверхность . Пусть в области D задано непрерывное векторное поле ,. Возьмем в этом векторном поле некоторую поверхностьS и выберем ее определенную сторону. Пусть – поле единичных нормалей к поверхности, соответствующее выбранной стороне. Тогда поверхностный интеграл 2-ого рода (т.к. )называется потоком вектора A через поверхность S в указанную сторону.

Пусть . Формула Гаусса-Остроградского:

Левую часть можно записать так: ,,. Следовательно:, так как. Это поток вектора через замкнутую поверхность. Правую часть можно записать какдивергенцию (расходимость ): .

Дивергенцией векторного поля A в точке MÎV называется производная функции по объему в этой точке:. Дивергенцию можно записать и с помощью оператора Набла : .Дивергенция в декартовых координатах : .

Свойства дивергенции:

Другие свойства (на лекции не разбирали, на усмотрение сдающего):

1. Соленоидальные векторные поля, условия соленоидальности.

Пусть в некоторой области D задано непрерывное векторное поле (M)=(x,y,z). Потоком векторного поля через ориентированную кусочно-гладкую поверхность S, расположенную в области D, называется интеграл , где – единичный вектор нормали к поверхности S, указывающий на ее ориентацию, а – элемент площади поверхности S.

Векторное поле называетсясоленоидальным в области D, если поток этого поля через любую кусочно-гладкую несамопересекающуюся поверхность , расположенную в D и представляющую собой границу некоторой ограниченной подобласти области D, равен нулю.

Если дивергенция равна нулю, то есть , то поле вектораназываетсясоленоидальным .

, поэтому поток везде, на каждом сечении трубки, одинаков.

Для того чтобы непрерывно дифференцируемое векторное поле былосоленоидальным в объемно-односвязной области D, необходимо и достаточно , чтобы во всех точках D выполнялось равенство . Где дивергенцией (“расходимость”) векторного поляназывается скалярная функция

"